Private Key and Public Key

In this article, we will discuss the private key and the public key, which form the foundation of bitcoin, and we will briefly mention addresses.

Topics covered in this article:

Private key (d)
Public key
Address
CSPRNG (Cryptographically Secure Pseudo Random Number Generator)
Elliptic Curve
secp256k1
Order (n)
Prime field (p)
Number of points (N)
Generator point (G)
Point at infinity (𝒪)
Modular inverse
Extended Euclidean Algorithm
Double-and-Add method
Public key point
Uncompressed public key
Compressed public key

In bitcoin, address generation begins with a large, randomly chosen number. From this number, we obtain the private key, then the public key, and finally the address, in that order.

Private key

↓

Public key

↓

Address

Random Number

There are various methods for generating random numbers. The simplest method is the PRNG (Pseudo Random Number Generator), but it is not secure. A more secure technique for cryptography is CSPRNG (Cryptographically Secure Pseudo Random Number Generator).

PRNG is usually called by functions like random() in programming languages. This method uses easily predictable data such as system time.

Using easily predictable data, such as system time, allows an attacker to guess the private key. If an attacker knows the time when the random() function was called, they can produce the same random number used in private key generation. Even if they don’t know the exact time, they can brute force a nearby time range. That is why it is not secure. Therefore, bitcoin and other cryptographic operations use CSPRNG instead of PRNG.

CSPRNG uses the operating system’s entropy pool. This pool contains data such as mouse movements, keyboard timing delays, and hardware-based randomness. It is almost impossible for an attacker to know these values, so they cannot reproduce the same random number.

In Python, the function secrets.randbits(k) generates a k-bit random number based on the CSPRNG method.

PRNG → Not secure
CSPRNG → More secure

(CSPRNG)

Random number

↓

Private key

↓

Public key

↓

Address

Private Key

A private key is a 256-bit randomly chosen number. The smallest selectable value is 1. It may look like the largest value is 2²⁵⁶-1, but it is actually one less than the order value (n) of the secp256k1 curve. We will explain terms like secp256k1 and order (n) later in this article.

2²⁵⁶ -1 = FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF
Order (n) = FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141

→ The selectable number range is 1 – (n-1).

We will now continue the article by creating an example script. Create a Python file named BitcoinKeyPairGenerator.py and write the following code into it. This code generates a 256-bit long random number using the CSPRNG method.

import secrets

def generate_private_key ():
    d = secrets.randbits(256)
    return d

private_key = generate_private_key()
print(private_key)

However, the code can also generate numbers larger than the order (n). To prevent this, we can use a while loop and continue selecting random numbers until we obtain a number smaller than the order (n). Applying mod_n directly in random number generation is not appropriate because this operation distorts the probability distribution and weakens security.

For example, suppose we choose a random number in the range 0–99 and apply mod₈₀. Without the modulus, every number has an equal chance of being selected. But after the modulus, the values 80–99 are mapped to the 0–19 range. In that case, numbers between 0–19 become more likely than those between 20–79. Such uneven distribution is an undesirable situation in cryptography.

import secrets

order_n = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141

def generate_private_key ():
    while(True):
        d = secrets.randbits(256)
        if(0 < d < order_n):
            return d

private_key = generate_private_key ()
print(private_key)

This update guarantees that only random numbers in the valid range are generated. Such a number can be used directly as a private key, and no further computation is required.

Public Key

A public key is generated from a private key using elliptic curve point multiplication.

Elliptic curve point multiplication is a one-way operation. In other words, it is possible to calculate which public key can be generated from a private key, but it is not possible to calculate which private key was used to generate a given public key. This property ensures that only the wallet owner can sign a bitcoin transfer, and this way, bitcoins cannot be stolen.

Note: Elliptic curve point multiplication should not be confused with ECDSA (Elliptic Curve Digital Signature Algorithm). Elliptic curve point multiplication is a mathematical operation, while ECDSA is an algorithm. Elliptic curve point multiplication is used to generate a public key from a private key. ECDSA is used for signing data with the private key and verifying the signature. Elliptic curve point multiplication is also performed in ECDSA, but not for generating public keys; instead, it is used for signing and verification. We will cover ECDSA in detail in later articles.

(CSPRNG)

Random number

↓

Private key

↓ − Elliptic curve

Public key

↓

Address

Elliptic Curve

The SECG (Standards for Efficient Cryptography Group) develops cryptographic methods and publishes them in SEC documents.

In cryptography, a type of curve called elliptic curve is used. There are various elliptic curves, each with its own formula. The elliptic curve used in bitcoin is secp256k1, and its formula is y² = x³ + 7 (mod_p).

In elliptic curve cryptography, every calculation with the curve formula is performed with the modulus p. This modulus is called the prime field (p). SEC curves are categorized by the approximate size of their prime field: 128-bit, 256-bit, 512-bit, and so on.

One such group is the secp256 family — the 256-bit group. This family includes three curves: secp256k1, secp256r1, secp256r2. All of them share the same general formula: y² = x³ + ax + b (mod_p).

For the secp256k1 curve, a = 0 and b = 7, and p is a very large number (specifically 2²⁵⁶ – 2³² – 977). We will discuss “p” in more detail later in this article.

y² = x³ + ax + b (mod_p) → General formula of secp256 family
secp256k1 → The curve used in bitcoin
a=0, b=7 → The predefined constants for secp256k1
y² = x³ + 7 (mod_p) → The elliptic curve formula used in bitcoin

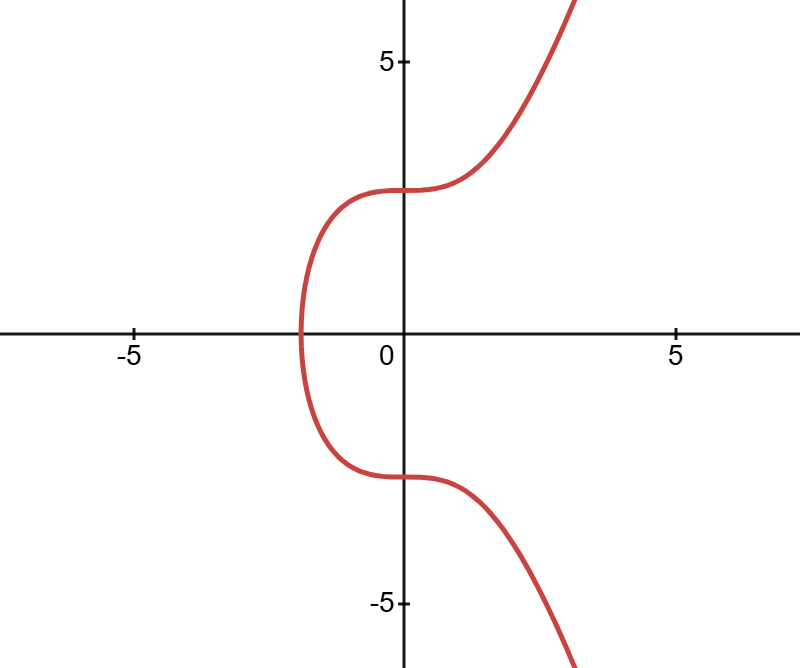
Points on the Elliptic Curve

As remembered from basic math, a point on a graph is represented by its (x, y) coordinates. These points can be visualized as vectors drawn from the origin to that point. Vectors can be added by connecting them end to end.

In cryptographic calculations, operations can also be performed with points on the graph, but only with points that lie on the elliptic curve.

Adding two points on the curve differs from vector addition. Instead, it is performed by determining the third point where the line passing through both points intersects the curve. The steps of this process are outlined below.

Choose two different points on the curve: P₁ and P₂, with P₁ ≠ P₂. If we draw a line through these two points and extend it to infinity, the line will intersect the curve at a third point (P₃). Reflecting P₃ across the x-axis results in point P₄. Point P₄ is defined as the sum of P₁ and P₂. Thus: P₁ + P₂ = P₄.

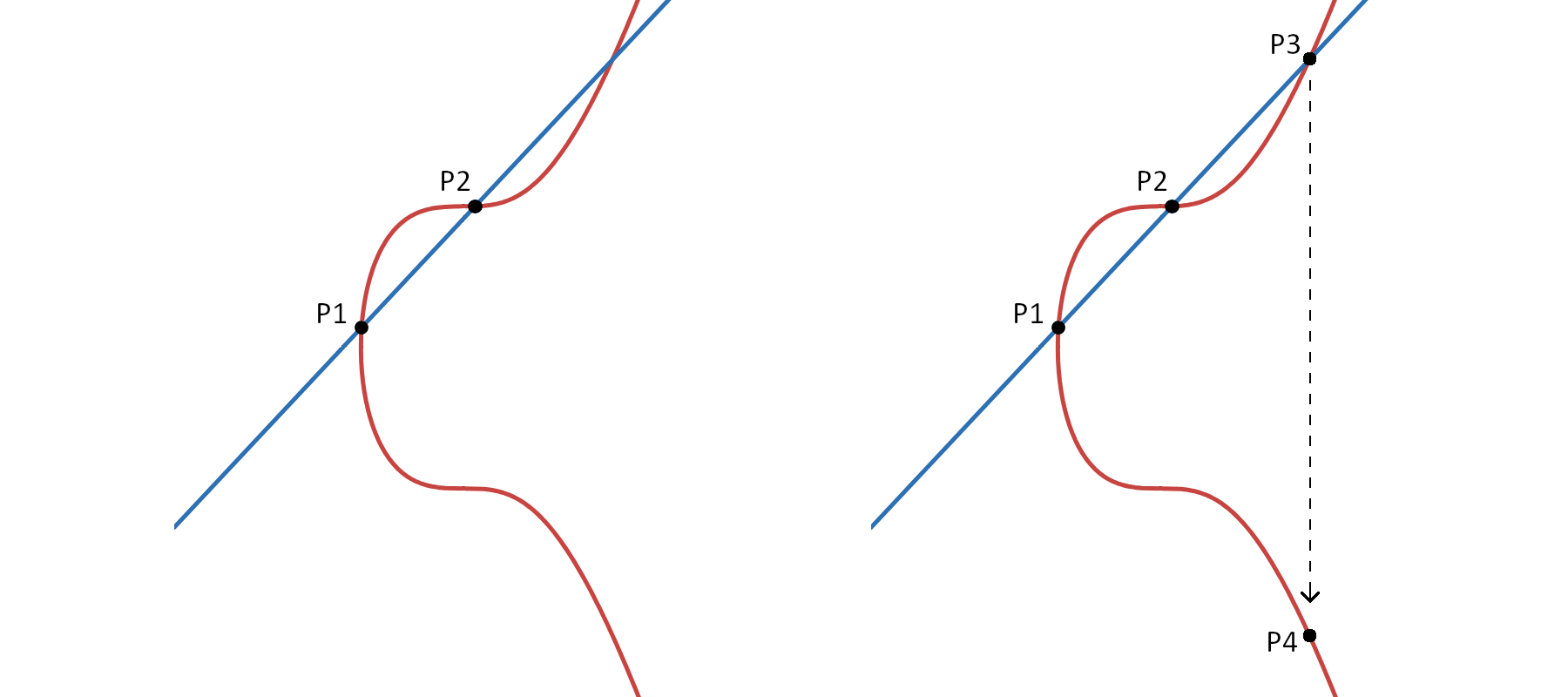
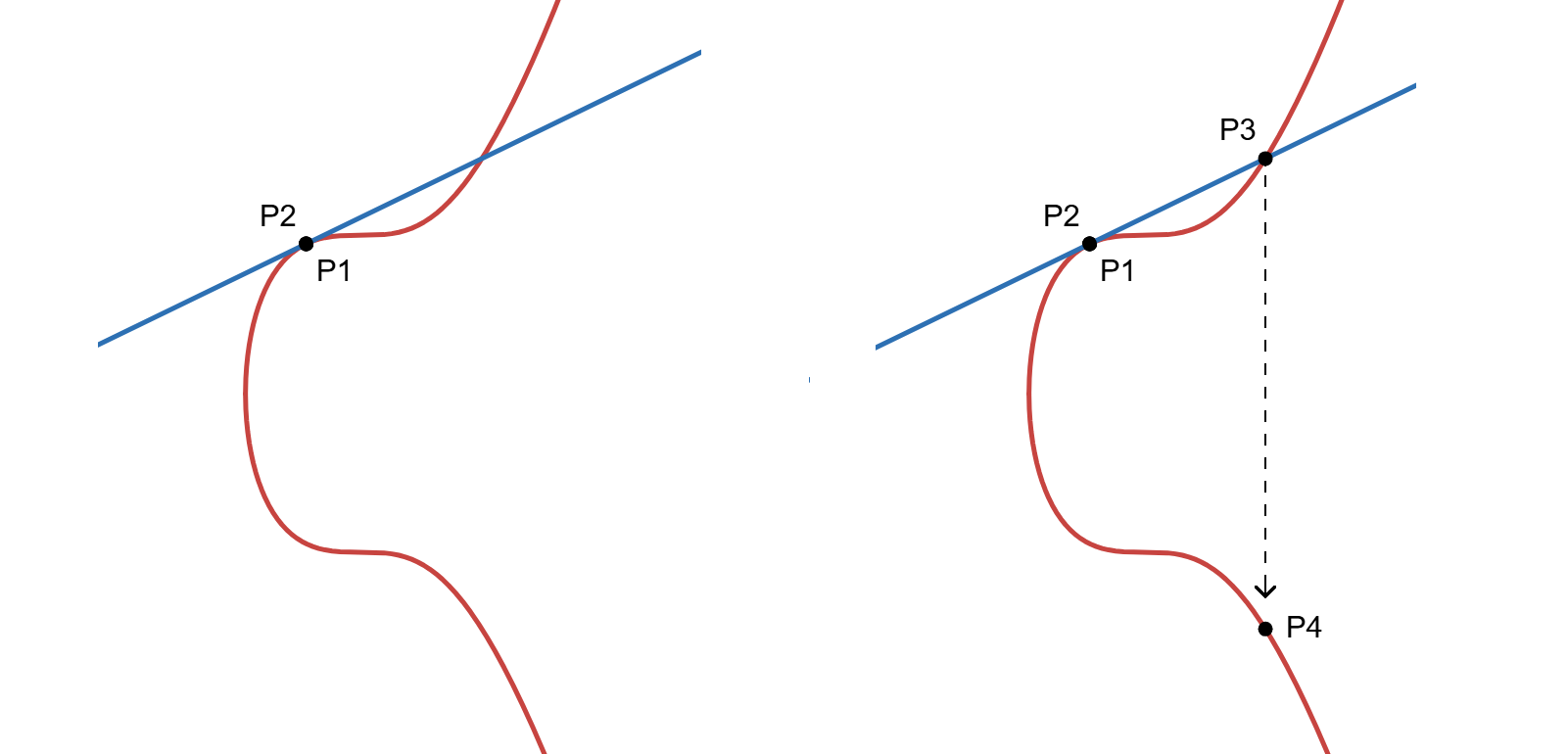
This method is only valid in the case where P₁ ≠ P₂. If P₁ = P₂, meaning the same point is being added, a tangent line is drawn to the curve at that point. Extending the tangent line to infinity, it intersects the curve at another point (P₃). Reflection of P₃ across the x-axis gives point P₄. Point P₄ is the sum of P₁ and P₂. Thus, P₁ + P₂ = P₄.

Prime Field (p)

In the examples above, the coordinates consist of continuous values (floating-point numbers). However, in cryptographic calculations, continuous values are not used; instead, positive integers are used, and these numbers are very large. For example, a private key is approximately 70 digits long.

Additionally, numbers cannot grow indefinitely — their maximum possible value is limited by the prime modulus (p). Calculations are performed using the mod_p operation. This ensures that all numbers remain within the range 0 – (p-1).

This value (p) is called the “prime field”, and it is a prime number. The prime field (p) value is very large, like the order (n) value, but it is not the same. These two numbers must not be confused.

2²⁵⁶ -1 = FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF
Order (n) = FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
Prime field (p) = FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F

So, why does the prime field (p) have this particular value? Because in cryptography, the prime field must be a large prime number. As the prime field value increases, the number of points on the curve also increases. This makes it harder for an attacker to guess private keys by brute force. Additionally, it must be prime for elliptic curve calculations to work correctly.

As explained in the earlier paragraphs, the secp256k1 curve uses a specific prime field (p) with the value shown above. This value was proposed by SECG. Therefore, for the secp256k1 curve, this prime field (p) value has become the standard.

For standardization, all calculations using the secp256k1 curve must use the same (p) value. Otherwise, if different (p) values are used, elliptic curve calculations will produce different public keys from the same private key, making signature verification impossible.

Number of Points (N)

On a graph, any point can be represented by an (x, y) combination, whether or not it lies on the curve. Some of these combinations satisfy the equation of the curve, and some do not.

When we consider continuous (floating-point) numbers such as (−1.90, 0.37), (0.23, 2.64), and (2.80, 5.39), marking all the points that satisfy the equation produces a continuous curve. This happens because continuous numbers are infinite, and thus there are infinitely many points that satisfy the equation.

However, in cryptography, we use positive integers instead of continuous numbers, and these integers also have a maximum value limit. This limit is the prime field (p). Therefore, both x and y values must fall within the range 0 – (p-1).

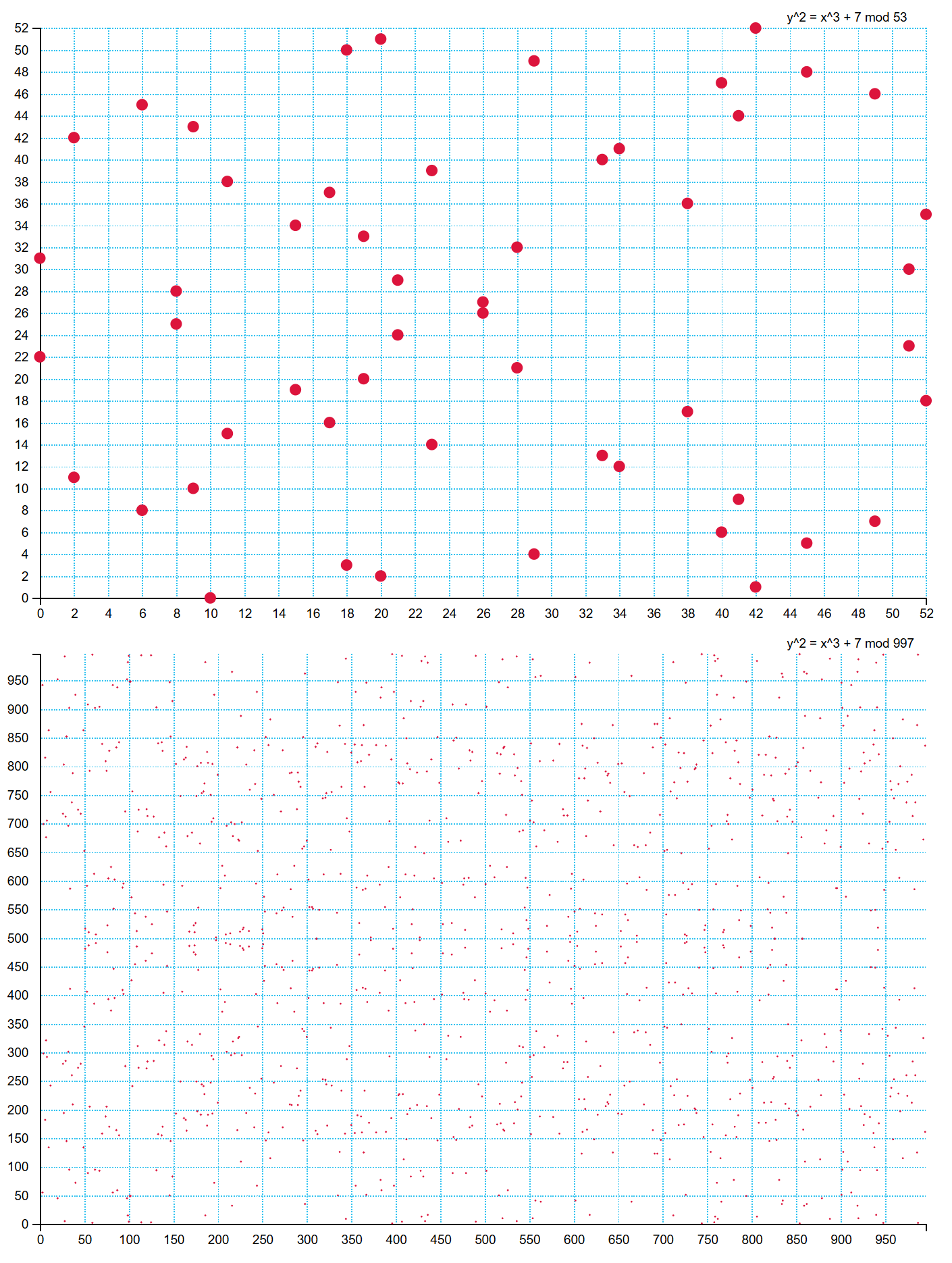
By choosing one number each for x and y within the prime field (p), we can form an (x, y) combination (a point). For example: (0,0), (0,1), (1,1), (2,1), (7,8), (25,16)… Some of these points satisfy the curve equation by mod_p, while others do not. The points that satisfy the equation form a set of valid points.

As shown in the example graphs, if p = 53, then there are 54 valid points. If p = 997, there are 1057 points. Since the p value used in bitcoin is very large, the number of points is also very large. It is impossible to plot all of them on a graph, which is why small prime values are used in examples.

It should also be noted that the number of points (N) is not the same as the order (n) or the prime field (p). These values must not be confused.

The number of points is usually close to the p value, but it does not have to be equal to it. It may be smaller or larger than p. There are algorithms to calculate the number of points, but to keep things simple, we will not delve into them here. The number of points on the elliptic curve used in bitcoin is approximately 1.158 × 10⁷⁷.

The figures show the distribution of points on the graph for fields with p = 53 and p = 997.

Elliptic Curve Arithmetic Operations

Cryptographic arithmetic operations are similar to the four basic operations, but with some differences. To make it easier to understand, the operations can be listed under separate headings:

Operations with numbers:
- Division (modular inverse)
- Addition
- Subtraction
- Multiplication
- Negation
Operations with points:
- Negation
- Doubling
- Addition
- Subtraction
Operation with point and number:
- Scalar multiplication

( / ) Modular Inverse

In cryptography, division is not performed in the same way as in basic mathematics. Instead, division is done by multiplying the dividend by its modular inverse. The modular inverse means the number that, when multiplied by “a” and then taken mod_p, gives a result of 1. That number is the modular inverse of “a”.

The modular inverse of a number is denoted as …^-1. For example, the modular inverse of “a” is written as a^-1.

So, how do we calculate this number a^-1? Brute force is practically impossible. Therefore, the Extended Euclidean Algorithm is used.

We won’t go into detail about the Extended Euclidean Algorithm here, but the process of calculating a modular inverse can be summarized as follows:

a –> number to invert
p –> prime field
q –> quotient
r –> remainder

p / a = q₁* a + r₁ x₁ = 0
a / r₁ = q₂* r₁ + r₂ x₂ = 1
r₁ / r₂ = q₃* r₂ + r₃ x₃ = x₁ – x₂* q₁
r₂ / r₃ = q₄* r₃ + r₄ x₄ = x₂ – x₃* q₂
r₃ / r₄ = q₅* r₄ + r₅ x₅ = x₃ – x₄* q₃
… / … = q_n* r_n-1 + r_n x_n = x_n-2 – x_n-1 * q_n-2 r_n = 0
—————————– x_n+1 = x_n-1 – x_n * q_n-1
——————————————————————————-
a^-1 = x_n+1

The process continues until r = 0.
After r = 0, one more x value is calculated.
The final calculated x value is the modular inverse of the number a.

( + – * ) Addition, Subtraction, Multiplication

These are normal addition, subtraction, and multiplication operations, except that the modulus must be applied at the end.

x + y = (x + y) mod_p

x – y = (x – y) mod_p

x * y = (x * y) mod_p

( -n ) Number Negation

Negation of a number is performed by subtracting it from (p). The important point here is that if the number is 0, its negative is also 0.

-x = (p – (x mod_p)) mod_p

( -P ) Point Negation

The negative of a point is found by taking the negative of its y coordinate. The negation of y is performed as explained above for numbers.

P = ( x , y )

-P = ( x , -y )

-P = ( x , p – (y mod_p) )

( P+P ) Point Doubling

Point doubling is the addition of a point to itself. The steps are:

Draw a tangent to the curve at P
The tangent intersects the curve at a third point: P₃
Reflect P₃ over the x-axis to get P₄
Result: P + P = P₄

( P₁+P₂ ) Point Addition

In point addition, if the points are different, the addition operation is performed. If the points are the same, the doubling operation is performed instead. The steps are:

Draw a line through both points (P₁ and P₂)
The line intersects the curve at a third point: P₃
Reflect P₃ over the x-axis to get P₄
Result: P₁ + P₂ = P₄

( P₁-P₂ ) Point Subtraction

Point subtraction is actually addition. Start by taking the negative of the point to be subtracted, then add it to the other point. If the resulting point after negation is the same as P₁, then the doubling operation is performed.

Take the negative of P₂
Then perform the addition: P₁ + (-P₂)

( k*P ) Scalar Multiplication

Multiplying a point by k is actually adding the point to itself k times: P + P + P + P… (k times). Since k is usually a very large number in cryptography, performing this addition one by one is impractical.

To speed up the calculation, the “Double-and-Add” method is used. As the first step, the number k is converted into binary form. Then, each bit is evaluated from left to right: if the bit is 0, perform doubling; if it is 1, perform doubling followed by addition.

Steps:

Convert k into binary format
Assign P to the starting point (M = P)
Begin processing the bits from the left, skipping the first bit
For each bit:
- If it is 0, perform doubling (M = 2M)
- If it is 1, perform doubling and then add P (M = 2M + P)

Example;

435 * P = ?
435 –> 110110011₂
110110011 –> ———– M₁ = P
110110011 –> M₁*2 + P = M₂
110110011 –> M₂*2 = M₃
110110011 –> M₃*2 + P = M₄
110110011 –> M₄*2 + P = M₅
110110011 –> M₅*2 = M₆
110110011 –> M₆*2 = M₇
110110011 –> M₇*2 + P = M₈
110110011 –> M₈*2 + P = M₉
435 * P = M₉

Point at Infinity (𝒪)

Recall the point addition method on the elliptic curve that we explained earlier. With this method, we added two different points that were not negatives of each other. But what happens if we add a point to its own negative? Since the positive and negative points are aligned on the same x-coordinate, the line through them will be vertical (parallel to the y-axis). Because of that, this vertical line will never intersect the curve at a third point.

Since there is no third intersection point, the addition does not result in a real point on the curve. Instead, the result of this addition is accepted to be an abstract point called the point at infinity (𝒪).

The point at infinity is the neutral element, meaning it acts as the identity element. In other words, it is like the number 0. When we add a number to 0, the result is the same number. When we subtract a number from 0, we get the negative of that number. When we multiply a number by 0, the result is always 0.

In elliptic curve mathematics, if we add a point to the point at infinity, the result is the same point. If we subtract a point from the point at infinity, we get the negative of that point. And if we apply scalar multiplication to the point at infinity, the result is still the point at infinity.

Order (n)

In the previous paragraphs, we mentioned the number of points (N) on the secp256k1 curve. Its approximate value is 1.158 × 10⁷⁷. The number of points can be divided by different cofactors (h) to form various subgroups (n). These subgroups are called the order (n).

N : number of points h : cofactor n: order

N = h * n

To avoid complicating the topic, we will not delve into the details of cofactors and subgroups. What’s important to know is that for the secp256k1 curve, h = 1. Therefore, for secp256k1, the order value (n) is equal to the number of points (N).

n = N

For cryptographic operations, the order (n) value must also be a prime number, just like the prime field (p), to ensure security. Since the number of points (N) on the secp256k1 curve is prime, and since h = 1, the order (n) value of the secp256k1 curve is also prime.

Attackers can also carry out brute-force attacks on subgroups (n) instead of on the entire point group (N). In other words, attackers can recover private keys by targeting these smaller subgroups rather than scanning the whole group. If the cofactor (h) is greater than one, multiple subgroups exist; as h increases, the number of points in the smallest subgroup decreases. Smaller subgroup sizes (a smaller number of points) make brute-force attacks easier. For this reason, it is preferable to have a single subgroup (h = 1), so that the subgroup size equals the total number of points.

Generator Point (G)

The G point is a standard starting point used to derive all public keys in bitcoin. In elliptic curve arithmetic, every public key is generated using the same G point. The only parameter that changes is the private key (d).

Since the G point is a point, it is represented by (x, y) coordinates. These coordinates, like p and n, are very large numbers. The standard G point used in the secp256k1 curve has the following coordinates:

G_x = 79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
G_y = 483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8

Mathematical origin of the G point

Multiplying a point by a number actually means repeatedly adding the point to itself. In other words: P * k = P + P + P + P + … (k times). At the end of these additions, under certain conditions, P_k becomes the point at infinity (𝒪).

How do we reach this point at infinity? As we continue adding, the point P_k-1 eventually becomes the negative of P₁. When P_k-1 is added to P₁ one final time, we reach P_k. Thus, the last step involves adding two opposite points; P_k becomes the point at infinity (𝒪).

P * k = 𝒪

With the appropriate choice of k, this equivalence can be satisfied for every point. In other words, depending on the chosen P point, the value of k changes.

In a (P, k) combination that satisfies this condition, if the value of k equals the order (n) of the secp256k1 curve, then that point P is called the Generator Point (G).

P * k = 𝒪 and k = n then P = G

Another detail is that even when k = n, more than one P point can satisfy the equation. So, multiple G points can exist. Which G point should be used in elliptic curve arithmetic? Any G point may be used. The important thing is that everyone must use the same G point. To ensure standardization in public key generation and signature verification, the same G point must be used in all calculations. Otherwise, different G points would result in different public keys from the same private key, making signature verification impossible.

How was the G point chosen?

The standard G point used in secp256k1, with the coordinates shown above, consists of very large numbers. It is impossible to start from 0 and find this point by incrementing the x and y coordinates one by one — it would take years. So, how was this G point found? The short answer is that it is not known.

In SEC documents published by SECG, the use of this G point was recommended for secp256k1. However, how these coordinates were found was not explained. Since SECG recommended it, this G point became the standard for secp256k1, and it serves as the base point for public key generation.

Because the exact origin of the standard G point is unknown, there are concerns that it could be a backdoor. However, no security vulnerability has been reported with the secp256k1 curve or the G point so far. What matters more than the origin of the G point is that everyone must use the same G point. Otherwise, standardization would break, and public key generation and signature verification would not be possible.

The importance of standardizing elliptic curve parameters

Based on the earlier explanations, it appears that the order (n) was calculated first, and then a suitable G point was chosen. IIn theory, there is no strict rule about how these parameters should be determined, but in practice, they are usually calculated in this sequence. To avoid unnecessary complexity, we will not go into theoretical details.

In practice, the steps for calculating elliptic curve parameters are as follows;

Select a large prime number for the prime field (p)
Calculate the number of points (N) (must be prime; if not, try a different p and recalculate N)
Calculate the order (n) (since h = 1, it equals N)
Choose one G point

The parameters p, a, b, N, h, n, G are all constant values. The only changing parameter is the private key (d), which is usually denoted by the letter d.

If any of the parameters p, a, b change, the number of points (N) in the prime field changes.
If N or h changes, the order value (n) changes.
If n changes, the G point changes.
If G point changes, the public keys generated from private keys (d) will change, and signature verification will not work.

The prime modulus p chosen in the first step could have been a different prime — the specific choice of prime is not essential. What matters is that everyone uses the same p, and this value must be prime and large enough to prevent brute force attacks.

Once a particular p is chosen, the parameters N and n are computed and a single generator point G is selected. Those parameters are then defined as the standard, and all elliptic-curve computations are performed based on this standard parameter set. If not everyone uses the same p, standardization is broken and public-key generation and signature verification will not work.

Implementing Elliptic Curve Arithmetics

In addition to the BitcoinKeyPairGenerator.py file we created earlier, create a file named EllipticCurveMath.py. To recall the constants we have discussed so far, let’s list them again and add them into the code file. Then, add a class to define points. Next, add the functions related to numbers: modulus, negation, and modular inverse. After that, add the functions required for points: negation, doubling, addition, and multiplication.

2²⁵⁶ -1 = FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF
Prime field (p) = FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
Order (n) = FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
G_x = 79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
G_y = 483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8

class Point:
    def __init__(self, x: int, y: int):
        self.x = x
        self.y = y

    def __eq__(self, other):
        if isinstance(other, Point):
            return self.x == other.x and self.y == other.y
        return False

    def __str__(self):
        return "x: {}\ny: {}".format(hex(self.x), hex(self.y))


# prime field
p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F

# order
n = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141

# generator point (x,y)
G = Point(
    0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798,
    0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8
)



# Mod operation
def mod(a:int) -> int:
    global p
    return a % p


# Negation of a number
def scalar_negate(a:int) -> int:
    return mod(p - mod(a))

# Modular inverse
def inverse(a:int) -> int:
    global p
    m=p
    original_m = m

    a = a % m
    if(a == 0):
        return None
    if(a == 1):
        return 1

    x1 = 0
    x2 = 1
    x3 = 0
    q3 = m // a
    r = m % a
    m = a
    a = r
    q1 = q3

    q3 = m // a
    r = m % a
    q2 = q3

    m = a
    a = r

    while (r > 0):
        q3 = m // a
        r = m % a

        x3 = (x1 - x2 * q1) % original_m
        x1 = x2
        x2 = x3
        q1 = q2
        
        q2 = q3
        m = a
        a = r
    
    x3 = (x1 - x2 * q1) % original_m
    return x3


# Negation of a point
def point_negate(pt:Point) -> Point:
    return Point(pt.x, scalar_negate(pt.y))


# Point doubling
def double(pt: Point) -> Point:
    s = mod((3*pt.x**2) * inverse(2*pt.y))
    x3 = mod(s**2 - 2*pt.x)
    y3 = mod(pt.y + s*(x3 - pt.x))
    pt3 = Point(x3,y3)
    return point_negate(pt3)


# Point addition
def add(pt1: Point, pt2: Point) -> Point:
    if(pt1 == pt2):
        return double(pt1)
    s = mod((pt2.y - pt1.y) * inverse(pt2.x - pt1.x))
    x3 = mod(s**2 - pt1.x - pt2.x)
    y3 = mod(s*(x3 - pt1.x) + pt1.y)
    pt3 = Point(x3,y3)
    return point_negate(pt3)


# Scalar multiplication
def multiply(pt: Point, k:int) -> Point:
    result = pt
    binary = bin(k)[2:]
    for b in binary[1:]:
        result = double(result)
        if(b == '1'):
            result = add(result, pt)
    return result

Generating the Public Key

The first step in generating a public key is scalar multiplication of the G point by the private key. The result of scalar multiplication is a point consisting of (x, y) coordinates.

P : public key point d : private key G : generator point

P = d * G

The x and y coordinates obtained from the public key point are written side by side in hexadecimal form to create the public key. This format is called the “uncompressed public key”. Alternatively, a “compressed public key” can also be generated.

To indicate the format of the public key, the following rules are applied.
– Uncompressed public key: “04” is placed at the beginning, followed by the x and y hexadecimal values written as strings without 0x.
– Compressed public key: Only the x value is written as a string. If y is even, “02” is placed at the beginning; if y is odd, “03” is placed.

In both cases, the numbers are in hexadecimal format. Concatenation is string concatenation, not mathematical addition. The “0x” prefix is not used at the start of the string values of x and y.

Public key_uncompressed : “04” + “P.x” + “P.y”
Public key_compressed : “02” + “P.x” (P.y mod₂ ≡ 0)
Public key_compressed : “03” + “P.x” (P.y mod₂ ≡ 1)

In practice, there is no actual need for the uncompressed public key. If x is known, the y value can be calculated from the elliptic curve formula. Two possible y values are obtained: one is positive and the other is negative. When we apply mod p to these two values as explained earlier, both become positive and smaller than p. One will be even and the other odd. Which value is used can be determined from the prefix “02” or “03”.

For this reason, compressed public keys are generally preferred when generating addresses.

Update our code file BitcoinKeyPairGenerator.py as shown below.

import secrets
import EllipticCurveMath as ecm


def generate_private_key():
    while(True):
        r = secrets.randbits(256)
        if(0 < r < ecm.n):
            return r
        

def generate_public_key(private_key:int):

    public_key_point = ecm.multiply(ecm.G, private_key)

    x_hex = format(public_key_point.x, "064x")
    y_hex = format(public_key_point.y, "064x")

    uncompressed_public_key_string = f"04{x_hex}{y_hex}"
    compressed_public_key_string = None
    if(public_key_point.y % 2 == 0):
        compressed_public_key_string = f"02{x_hex}"
    else:
        compressed_public_key_string = f"03{x_hex}"

    return (public_key_point, uncompressed_public_key_string, compressed_public_key_string)



# private key
private_key = generate_private_key()
print("d: {}".format(hex(private_key)))


# public key
(public_key_point, uncompressed_public_key_string, compressed_public_key_string) = generate_public_key(private_key)
print(public_key_point)
print("uncompressed_public_key:\t{}".format(uncompressed_public_key_string))
print("compressed_public_key:\t{}".format(compressed_public_key_string))

Address

Addresses are derived from the public key. In fact, it is not mandatory to use addresses in bitcoin transfers; public keys can also be used directly. However, in modern implementations, addresses are preferred to increase privacy, shorten the character length, and improve readability.

The term “address” can sometimes be confusing. In bitcoin, an address usually refers to the string derived from the public key. But sometimes the term is also used to describe the target bitcoin will be sent to. This target is usually in address format, but it can also be a public key.

Therefore, the term ‘address’ may sometimes refer to the public key itself or to the address derived from it.

We will cover the methods of address generation, address formats, and their purposes in detail in later articles.

(CSPRNG)

Random number

↓

Private key

↓ − Elliptic curve

Public key

↓ − Address generation methods

Address

Final Thoughts

In this article, we have explained the concepts of private key and public key in detail, which form the foundation of bitcoin. In the next article, we’ll talk about addresses.

I wish you a life that makes a difference.

Private key

↓

Public key

↓

Address

Random Number

(CSPRNG)

Random number

↓

Private key

↓

Public key

↓

Address

Private Key

Public Key

(CSPRNG)

Random number

↓

Private key

↓ − Elliptic curve

Public key

↓

Address

Elliptic Curve

Points on the Elliptic Curve

Prime Field (p)

Number of Points (N)

Elliptic Curve Arithmetic Operations

( / ) Modular Inverse

( + – * ) Addition, Subtraction, Multiplication

( -n ) Number Negation

( -P ) Point Negation

( P+P ) Point Doubling

( P1+P2 ) Point Addition

( P1-P2 ) Point Subtraction

( k*P ) Scalar Multiplication

Point at Infinity (𝒪)

Order (n)

Generator Point (G)

Mathematical origin of the G point

How was the G point chosen?

The importance of standardizing elliptic curve parameters

Implementing Elliptic Curve Arithmetics

Generating the Public Key

Address

(CSPRNG)

Random number

↓

Private key

↓ − Elliptic curve

Public key

↓ − Address generation methods

Address

Final Thoughts

( P₁+P₂ ) Point Addition

( P₁-P₂ ) Point Subtraction