Bu yazıda bitcoinin temelini oluşturan özel anahtar (private key) ve açık anahtar (public key) konularını ele alacağız ve adreslere kısaca değineceğiz.
Yazımızda bahsi geçen kavramlar:
- Private key (özel anahtar) (d)
- Public key (açık anahtar)
- Address (adres)
- CSPRNG (Cryptographically Secure Pseudo Random Number Generator)
- Elliptic Curve (eliptik eğri)
- secp256k1
- Order (n)
- Prime field (p)
- Nokta sayısı (N)
- Generator point (G)
- Point at Infinity (𝒪)
- Modular inverse
- Extended Euclidean Algorithm (Genişletilmiş Öklid Algoritması)
- Double-and-Add yöntemi
- Public key point
- Uncompressed public key
- Compressed public key
Bitcoinde adres üretimi rastgele seçilen büyük bir sayıyla başlar. Bu sayıdan sırayla önce private key, sonra public key ve en sonunda adres elde edilir.
Private key
↓
Public key
↓
Address
Random Sayı
Rastgele sayı üretmek için farklı yöntemler vardır. En basit olanı PRNG (Pseudo Random Number Generator) yöntemidir ama güvenli değildir. Kriptografi için daha güvenli olan yöntem ise CSPRNG (Cryptographically Secure Pseudo Random Number Generator) yöntemidir.
PRNG, genelde programlama dillerindeki random() gibi fonksiyonlarla çağrılır. Bu yöntem, sistem zamanı gibi kolay tahmin edilebilen verileri kullanır. Bu yüzden güvenli değildir.
Sistem zamanı gibi kolay tahmin edilebilir verileri kullanması, saldırganın private key’i tahmin edebilmesine yol açar. Örneğin saldırgan, random() fonksiyonunun çağrıldığı zamanı biliyorsa private key üretiminde kullanılan aynı random sayıyı üretebilir. Zamanı tam bilmezse bile yakın bir zaman aralığını brute force ile deneyebilir. Bu yüzden bitcoin ve diğer kriptografik işlemlerde PRNG yerine CSPRNG kullanılır.
CSPRNG, işletim sisteminin entropi havuzunu kullanır. Bu havuzda; fare hareketleri, klavye gecikmeleri, donanım tabanlı rastgelelik gibi veriler bulunur. Saldırganın bu verileri bilmesi neredeyse imkânsızdır, dolayısıyla aynı random sayıyı üretemez.
Python’da secrets.randbits(k) fonksiyonu, CSPRNG yöntemine uygun şekilde k-bitlik random sayı üretir.
- PRNG → Güvenilir değil.
- CSPRNG → Daha güvenli.
(CSPRNG)
Random number
↓
Private key
↓
Public key
↓
Address
Private Key
Private key, 256 bitlik random seçilen bir sayıdır. Seçilebilecek en küçük değer 1’dir. En büyük değer ise sanılanın aksine 2256-1 değil; secp256k1 eğrisinin order değeri (n)’nin bir eksiğidir. Secp256k1, order (n) gibi terimleri yazının ilerleyen kısımlarında açıklayacağız.
- 2256 -1 = FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF
- Order (n) = FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
→ Seçilebilecek sayı aralığı 1 – (n – 1) arasıdır.
Yazımıza örnek bir script oluşturarak devam edelim. BitcoinKeyPairGenerator.py adında bir Python dosyası oluşturalım ve içine aşağıdaki kodu yazalım. Bu kod, CSPRNG yöntemiyle 256-bit uzunluğunda random bir sayı üretir.
import secrets
def generate_private_key ():
d = secrets.randbits(256)
return d
private_key = generate_private_key()
print(private_key)
Ancak bu kodda, order (n) değerinden büyük sayılar da üretilmektedir. Bunu önlemek için bir while döngüsü kullanabilir ve sadece n değerinden küçük bir sayı elde edilene kadar random sayı seçimine devam edebiliriz. Rastgele sayı üretiminde doğrudan modn işlemi uygulanması uygun değildir, çünkü bu işlem olasılık dağılımını bozar ve güvenliği zayıflatır.
Örneğin 0–99 aralığında random sayı seçtiğimizi ve mod80 uyguladığımızı düşünelim. Mod alınmazsa her sayının seçilme olasılığı eşittir. Ancak mod80 sonrası 80–99 arası değerler 0–19 aralığına eklenir. Bu durumda 0–19 arasındaki sayıların seçilme olasılığı 20-79 aralığına göre daha fazla olur. Bu da kriptografide istenmeyen bir durumdur.
import secrets
order_n = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
def generate_private_key ():
while(True):
d = secrets.randbits(256)
if(0 < d < order_n):
return d
private_key = generate_private_key ()
print(private_key)
Koddaki bu güncellemeyle, artık yalnızca geçerli aralıkta random sayı seçilmektedir. Bu random sayıyı doğrudan private key olarak kullanabiliriz; başka işleme gerek yoktur.
Public Key
Public key, private key üzerinden eliptik eğri hesaplamalarıyla oluşturulur.
Eliptik eğrideki hesaplamalar, tek yönlü işlemlerdir. Yani private key’den hangi public key oluşturulabileceği hesaplanabilir ancak tersi şekilde public key’in hangi private key’den oluşturulmuş olduğu hesaplanamaz. Bu özellik sayesinde bitcoin transferinin sadece cüzdan sahibi tarafından imzalanması sağlanmış olur ve böylece bitcoinlerin çalınması önlenmiş olur.
Not: Eliptik eğri hesaplaması, ECDSA (Elliptic Curve Digital Signature Algorithm) ile karıştırılmamalıdır. Eliptik eğri hesaplaması matematiksel bir işlem iken, ECDSA bir algoritmadır. Eliptik eğri hesaplaması, private key’den public key üretmek için kullanılır. ECDSA ise private key ile veri imzalama ve imzayı doğrulama işlemlerinde kullanılır. ECDSA’da da eliptik eğri hesaplamaları yapılır ancak public key oluşturmak amacıyla değil veri imzalama ve doğrulama amacıyla yapılır. ECDSA konusunu sonraki yazılarımızda ayrıntılı şekilde ele alacağız.
(CSPRNG)
Random number
↓
Private key
↓ − Eliptik eğri
Public key
↓
Address
Eliptik Eğri
SECG (Standards for Efficient Cryptography Group) tarafından kriptografide kullanılması amacıyla yöntemler geliştirilmektedir ve bu yöntemler SEC dökümanlarında yayınlanmaktadır.
Kriptografik hesaplamalarda eliptik eğri adı verilen eğri türleri kullanılır. Çeşitli eğriler bulunmaktadır ve her birinin formülü farklıdır. Bitcoinde kullanılan eğri, secp256k1 eğrisidir ve bu eğrinin formülü şudur: y² = x³ + 7 (modp).
Kriptografide eğri formülüyle yapılan tüm hesaplamalarda modül alma (modp) işlemi uygulanır. Bu modüle alan modülü (p, prime field) denir. Secp eğrileri, alan modülünün yaklaşık büyüklüğüne göre sınıflandırılır: 128-bit, 256-bit, 512-bit vs.
Bu kategorilerden biri de 256-bit eğri grubu olan secp256 grubudur. Bu grupta üç farklı eğri türü bulunur: secp256k1, secp256r1, secp256r2. Hepsinin formülü ortaktır ve formülü şudur: y² = x³ + ax + b (modp).
Farklı olan, a, b ve p parametrelerinin değerleridir. secp256k1 eğrisi için a = 0 ve b = 7’dir. Alan modülü olan p değeri ise çok büyük bir sayı (tam olarak 2256 – 232 – 977 değerinde) olup bu p sayısını yazının ilerleyen kısımlarında daha ayrıntılı ele alacağız.
- y2 = x3 + ax + b (modp) → secp256 eğri grubunun genel formülü
- secp256k1 → Bitcoinde kullanılan eliptik eğri türü
- a=0, b=7 → secp256k1 eğrisinin sabit değerleri
- y2 = x3 + 7 (modp) → Bitcoinde kullanılan eliptik eğri formülü
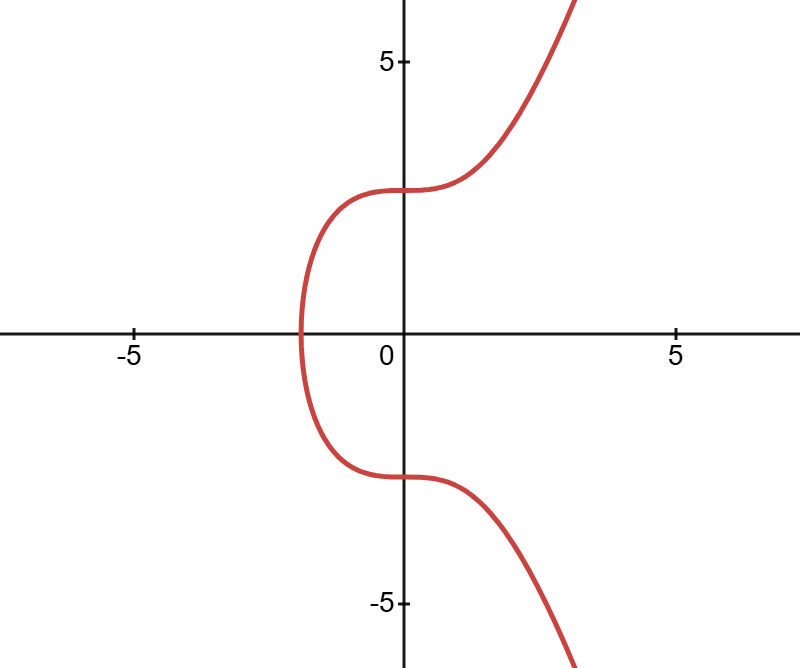
Eğri Üzerindeki Noktalar
Temel matematik bilgisinden hatırlanacağı üzere grafik üzerinde bir nokta, (x, y) koordinatlarıyla gösterilir. Bu noktalar, sıfır noktasından başlayıp ilgili noktaya kadar uzanan vektörler gibi düşünülebilir. Vektörler uç uca eklenerek toplanabilir.
Kriptografik hesaplamalarda da grafik üzerindeki noktalarla işlem yapılabilir ancak sadece eliptik eğri üzerine denk gelen noktalarla hesaplama yapılabilir. Eğri üzerindeki iki noktanın toplamı, vektörlerdeki gibi uç uca eklenerek değil; her iki noktadan geçen doğrunun eğriyi kestiği üçüncü nokta bulunarak yapılır. Şimdi bu işlemi açıklayalım.
Eğri üzerinde bulunan iki farklı nokta seçelim: P1 ve P2. Yani P1 ≠ P2. Bu iki noktadan geçen bir doğru çizip uçlarını sonsuza doğru uzatırsak, bu doğru eğriyle üçüncü bir noktada (P3) kesişir. P3 noktasının x eksenine göre simetriğini aldığımızda elde edilen nokta P4 olur. P4 noktası, P1 ve P2’nin toplamıdır. Yani P1 + P2 = P4.
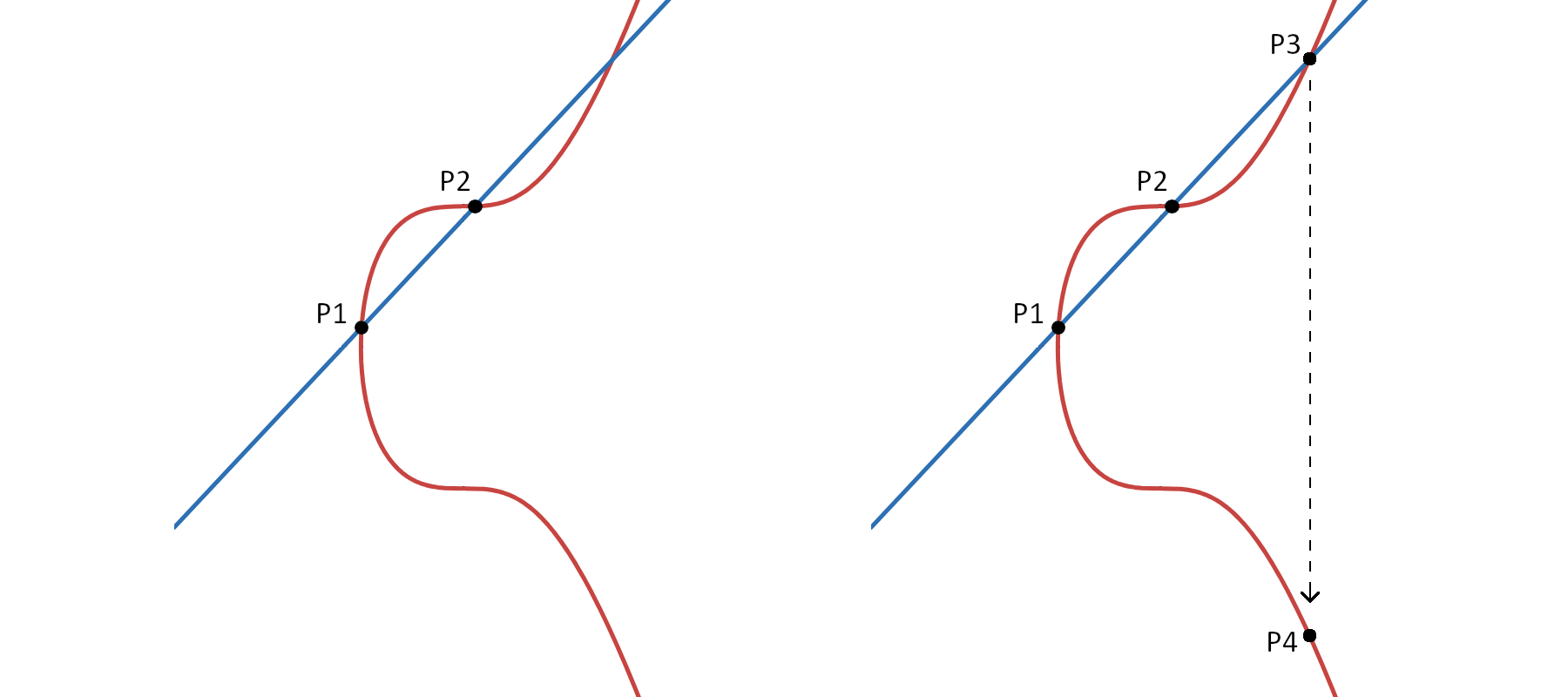
Bu yöntem yalnızca P1 ≠ P2 durumunda geçerlidir. Eğer P1 = P2 ise, yani aynı nokta iki kez toplanacaksa, bu noktadan eğriye teğet bir doğru çizilir. Teğet doğrusunun uçlarını sonsuza doğru uzatırsak, bu teğet eğriyle başka bir noktada (P3) kesişir. P3 noktasının x eksenine göre simetriğini aldığımızda elde edilen nokta P4 olur. P4 noktası, P1 ve P2’nin toplamıdır. Yani P1 + P2 = P4.
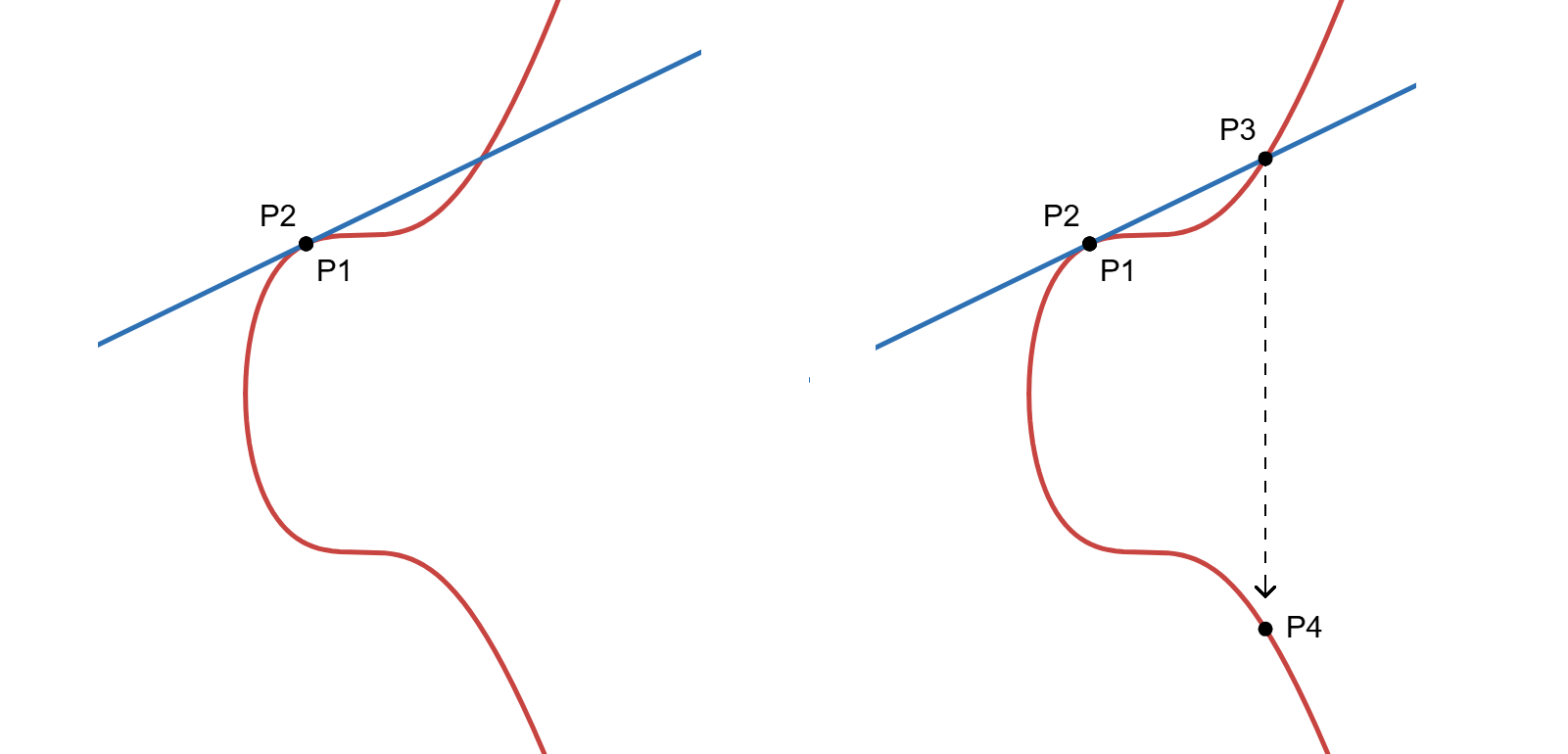
Prime Field (p)
Yukarıdaki örneklerde koordinatları, reel (gerçek) sayılardan oluşan noktalar kullanılmaktadır. Oysa, kriptografik hesaplamalarda reel sayılar değil pozitif tam sayılar kullanılır ve bu sayılar çok büyük sayılardır. Örneğin, private key yaklaşık 70 basamaklı bir sayıdır.
Ayrıca, sayıların alabileceği maksimum bir sınırı vardır. Maksimum sınır, asal sayı modülüdür (p). Hesaplamalarda modp işlemi uygulanır. Böylece tüm sayıların 0 – (p-1) aralığında olması sağlanır.
Bu (p) değerine “alan modülü” (prime field) denir ve bir asal sayıdır. Prime field (p) değeri, order değeri (n) gibi çok büyük bir değerdir, ancak ondan farklıdır. Bu iki sayı karıştırılmamalıdır.
- 2256 -1 = FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF
- Order (n) = FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
- Prime field (p) = FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
Peki, prime field (p) neden yukarıda belirtilen bu değere sahiptir? Çünkü kriptografide kullanılan prime field’ın bir asal sayı olması ve oldukça büyük olması gerekir. Prime field değeri büyüdükçe nokta sayısı artar ve artan nokta sayısı brute force yöntemi ile private key’lerin saldırganlar tarafından tahmin edilmesini zorlaştırır. Kriptografik hesaplamaların yapılabilmesi için de asal sayı olması gerekir.
Önceki paragraflarda açıklandığı gibi secp256k1 eğrisinde prime field (p) değeri sabittir ve yukarıdaki yazılı değerdir. Bu değer, SECG tarafından önerilmiştir. Bu nedenle secp256k1 eğrisinde bu prime field (p) değeri standart hale gelmiştir.
Standizasyon için secp256k1 eğrisini kullanan tüm hesaplamaların aynı (p) değerini kullanması gerekir. Aksi halde farklı (p) değerleri kullanılırsa eliptik eğri hesaplamalarında aynı private key’den farklı public key’ler oluşur ve imza doğrulama mümkün olmaz.
Nokta Sayısı (N)
Grafik üzerinde herhangi bir nokta eğri üzerinde olsun yada olmasın (x,y) kombinasyonu ile gösterilir. Bu kombinasyonlardan bazıları formüldeki denkliği sağlayan kombinasyonlardır. Reel sayı kapsamında incelersek, örneğin; (-1.90, 0.37), (0.23, 2.64), (2.80, 5.39)… noktaları gibi denklem denkliğini sağlayan tüm noktaları grafik üzerinde işaretlersek kesintisiz bir eğri ortaya çıkar, çünkü reel sayılar sonsuz olduğu için denklemi sağlayan sonsuz sayıda nokta vardır.
Ancak kriptografide reel sayılarla değil, pozitif tam sayılarla işlem yapılır ve bu tam sayıların da maksimum sınırı vardır. Bu sınır prime field (p) değeridir. Yani x ve y değerleri 0 – (p-1) aralığında olmak zorundadır.
Hem x hem de y için prime field (p) içerisinden birer sayı seçerek (x,y) kombinasyonu (nokta) oluşturabiliriz. Örneğin (0,0), (0,1), (1,1), (2,1), (7,8), (25,16)… Bu noktalardan bazıları modp ile denklem denkliğini sağlarken bazıları sağlamaz. Denkliği sağlayan noktaları grafik üzerinde işaretlediğimizde bir nokta kümesi elde ederiz. Örnek grafiklerde görülebileceği üzere p değerini 53 olarak seçersek denkliği sağlayan 54 nokta olur. p = 997 seçildiğinde ise 1057 nokta olur. Bitcoinde kullanılan p çok büyük olduğu için nokta sayısı da çok fazladır. Bu kadar noktayı grafik üzerinde göstermek imkânsızdır. Bu yüzden, p değerini küçük sayılar seçerek örnek gösterdik.
Ayrıca dikkat edilmelidir ki nokta sayısı (N); order (n) veya prime field (p) sayıları değildir, bunlarla karıştırılmamalıdır.
Nokta sayısı, genellikle p değerine yakındır fakat tam olarak p’ye eşit olması gerekmez. p’den küçük ya da büyük olabilir. Nokta sayısını bulmak için bazı algoritmalar mevcuttur ancak konuyu dağıtmamak için burada değinmeyeceğiz. Bitcoinde kullanılan eliptik eğrideki nokta sayısı yaklaşık 1.158 × 1077’dir.
Görseller, p = 53 ve p = 997 alanlarındaki noktaların grafikteki dağılımlarını göstermektedir.
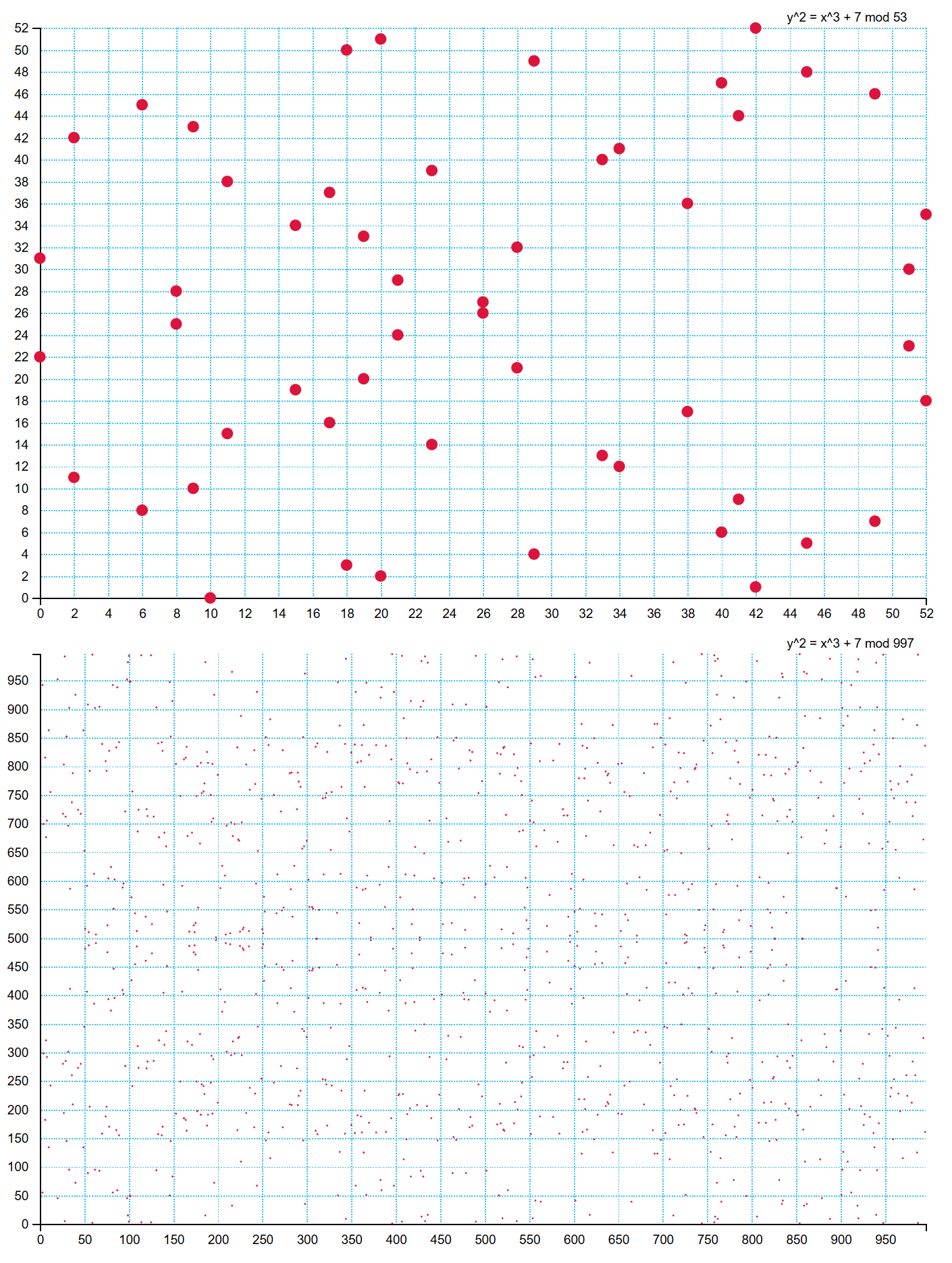
Eliptik Eğrideki Matematiksel İşlemler
Prime field’deki tam sayılarla yapılan kriptografik işlemler, reel sayılarla yapılan dört işleme benzerdir ancak bazı farklılıklar vardır. Daha kolay anlaşılabilmesi için öncelikle işlemleri başlıklar halinde sıralayalım;
- Sayılarla yapılan işlemler
- Bölme (Modüler Ters [Modular Inverse])
- Toplama
- Çıkarma
- Çarpma
- Negatif alma
- Noktalarla yapılan işlemler
- Negatif alma
- Çiftleme (Double)
- Toplama
- Çıkarma
- Sayı ve noktanın birlikte kullanıldığı işlemler
- Skalar çarpma
( / ) Modular Inverse
Kriptografide bölme işlemi temel matematikteki gibi yapılmaz, bunun yerine bölünen sayının p değerine göre modüler tersi alınır. Modüler tersin anlamı şudur: örneğin “a” sayısını hangi sayı ile çarparsak ve çarpım sonucuna modp işlemi uygularsak sonuç “1” çıkar? İşte cevabını bulmak istediğimiz sayı “a” sayının modüler tersidir. Bir sayının modüler tersini ifade etmek için …-1 gösterimi kullanılır. Örneğin, “a” sayının modüler tersi a-1 şeklinde gösterilir.
Peki, bu a-1 sayısı nasıl hesaplanır? Brute force yöntemi pratikte imkansızdır. Bu nedenle Genişletilmiş Öklid Algoritması (Extended Euclidean Algorithm) kullanılır.
Yazıyı uzatmamak için genişletilmiş öklid algoritmasının ayrıntılarına değinmeyeceğiz. Bir sayının modüler tersinin hesaplanması özetle aşağıdaki şekilde yapılır;
a –> modüler tersi aranan sayı
p –> prime field
q –> bölüm (quotient)
r –> kalan (remainder)
- p / a = q1 * a + r1 x1 = 0
- a / r1 = q2 * r1 + r2 x2 = 1
- r1 / r2 = q3 * r2 + r3 x3 = x1 – x2 * q1
- r2 / r3 = q4 * r3 + r4 x4 = x2 – x3 * q2
- r3 / r4 = q5 * r4 + r5 x5 = x3 – x4 * q3
- … / … = qn * rn-1 + rn xn = xn-2 – xn-1 * qn-2 rn = 0
- —————————– xn+1 = xn-1 – xn * qn-1
- ——————————————————————————-
- a-1 = xn+1
r=0 olana kadar işlem tekrarlanır.
r=0 olduktan sonra son bir kez daha x değeri hesaplanır.
Hesaplanan nihai x değeri a sayısının modüler tersidir.
( + – * ) Toplama, Çıkarma, Çarpma
Bu işlemler normal toplama, çıkarma ve çarpma işlemleridir. İlaveten yapılması gereken işlemlerden sonra modül alınmasıdır.
x + y = (x + y) modp
x – y = (x – y) modp
x * y = (x * y) modp
( -n ) Negatif Alma
Negatif alma işlemi sayının (p) değerinden çıkarılmasıdır. Dikkat edilmesi gereken eğer sayı 0 ise negatifi de 0’dır.
-x = (p – (x modp)) modp
( -P ) Noktanın Negatifini Alma
Noktanın negatifi y eksenindeki değerin negatifi alınarak yapılır. y’nin negatifini alma işlemi ise yukarıda açıklandığı gibi sayının negatifi alma yöntemi kullanılarak yapılır.
P = ( x , y )
-P = ( x , -y )
-P = ( x , p – (y modp) )
( P+P ) Nokta Çiftleme
Nokta çiftleme, bir noktanın kendisiyle toplamıdır. Adımlar şöyledir;
- P’den eğriye teğet geçen doğru çizilir
- Teğetin eğriyi kestiği nokta bulunur (P3)
- P3’ün x eksenine göre simetriği alınır (P4)
- Çiftleme işleminin sonucu simetrik nokta P4’tür.
- P + P = P4
( P1+P2 ) Nokta Toplama
Nokta toplamada noktalar farklı ise toplama işlemi yapılır. Eğer noktalar aynı nokta ise toplama yerine çiftleme işlemi yapılır. Toplama işleminin adımları şöyledir;
- P1 ve P2’den geçen bir doğru çizilir
- Bu doğrunun eğriyi kestiği üçüncü nokta bulunur (P3)
- P3’ün x eksenine göre simetriği alınır (P4)
- Toplama işleminin sonucu simetrik nokta P4’tür.
- P1 + P2 = P4
( P1-P2 ) Nokta Çıkarma
Nokta çıkarma, aslında toplama işlemidir. Önce çıkarılacak noktanın negatifi alınır, ardından diğer noktayla toplanır. Eğer P2’nin negatifi alındıktan sonra elde edilen nokta P1 ile aynı nokta olursa çiftleme işlemi yapılır.
- P2’nin negatifi alınır (-P2)
- P1 + (-P2) toplama işlemi yapılır
( k*P ) Skalar Çarpma
Bir noktanın k ile çarpılması, aslında k kez kendisiyle toplanmasıdır. P+P+P+P…(k kez). Ancak kriptografide çok büyük sayılarla işlem yapıldığı için toplama işlemini tek tek yapmak pratikte imkansızdır.
Hesaplama sürecini hızlandırmak için “Double-and-Add” yöntemi kullanılır. Bu yöntemi uygulamak için “k” sayısı binary formata çevrilir. Ardından soldan başlanarak bit değerinin 0 ya da 1 olmasına göre P noktası için çiftleme veya toplama yapılır. Yöntemin uygulanışı şu şekildedir;
- k, binary formata çevrilir
- Başlangıç noktasına (M) değer olarak P noktası atanır (M=P)
- Bit değerlerini işlemeye soldan başlanır ve ilk bit atlanır
- Sonra gelen bit değerlerine göre;
- 0 ise çiftleme yapılır (M = 2*M)
- 1 ise çiftleme yapılır ve ardından P ile toplanır (M = 2*M + P)
Örnek;
- 435 * P = ?
- 435 –> 1101100112
- 110110011 –> ———– M1 = P
- 110110011 –> M1*2 + P = M2
- 110110011 –> M2*2 = M3
- 110110011 –> M3*2 + P = M4
- 110110011 –> M4*2 + P = M5
- 110110011 –> M5*2 = M6
- 110110011 –> M6*2 = M7
- 110110011 –> M7*2 + P = M8
- 110110011 –> M8*2 + P = M9
- 435 * P = M9
Point at Infinity (𝒪)
Daha önce anlattığımız eliptik eğri üzerinde yapılan nokta toplama yöntemini hatırlayalım. Bu yöntemle birbirlerinin negatifi olmayan farklı noktaları toplamıştık. Eğer bir noktayı kendisinin negatifi ile toplarsak pozitif ve negatif noktalar x ekseninde aynı konumda olduklarından dolayı noktalardan geçen bir doğru çizildiğinde doğru y eksenine paralel olur. Bu nedenle; doğru, eğriyle üçüncü bir noktada asla kesişmez. Üçüncü noktayla kesişme olmadığından dolayı toplama sonucunda gerçek bir nokta elde edilemez. Toplama işlemi sonucunun soyut bir nokta olan sonsuzdaki nokta (𝒪) olduğu kabul edilir.
Sonsuzdaki nokta nötr elemandır, yani etkisiz elemandır. Diğer bir deyişle 0 sayısı gibidir. Bir sayıyı 0 ile topladığımızda sonuç gene aynıdır. Sayıyı, 0’dan çıkardığımızda ise sayının negatifini elde ederiz. Çarpma işleminde ise sonuç 0’dır. Eliptik eğri matematiğinde de bir noktayı sonsuz nokta ile topladığımızda sonuç gene aynı nokta olur. Noktayı, sonsuzdaki noktadan çıkardığımızda noktanın negatifini elde ederiz. Sonsuzdaki noktaya skalar çarpma işlemi uyguladığımızda sonuç gene sonsuzdaki noktadır.
Order (n)
Önceki paragraflarda secp256k1 eğrisindeki nokta sayısından (N) bahsetmiştik. Yaklaşık değeri 1.158 × 1077’dir. Bu nokta sayısı farklı kofaktörlere (h) bölünerek çeşitli alt gruplara ayrılabilir (n). Bu alt gruplara order (n) denir. Türkçe ifadesi “grup mertebesi” dir.
N : nokta sayısı h : kofaktör n: order değeri
N = h * n
Konuyu daha karmaşık hale getirmemek için kofaktör ve alt grubun ne olduğuna dair ayrıntılara değinmeyeceğiz. Bilinmesi gereken secp256k1 eğrisi için h=1’dir. Dolayısıyla secp256k1 eğrisinde order değeri (n), nokta sayısına (N) eşit olur.
n = N
Kriptografik işlemlerde güvenliği sağlamak amacıyla, order (n) değerinin de prime field (p) değeri gibi bir asal sayı olması gerekir. Secp256k1 eğrisindeki nokta sayısı (N) asal sayı olduğu için ve h=1 olduğu için secp256k1 eğrisindeki order (n) değeri de asal sayı olmuş olur.
Private key’i tahmin etmek için tüm nokta grubu (N) yerine altgruplar (n) üzerinde de brute force saldırıları yapılabilir. Yani, saldırganlar, tüm nokta grubunu taramadan daha küçük bu altgrupları tarayarak da private key’leri bulabilirler. Eğer kofaktör birden büyük olursa birden fazla alt grup olur ve kofaktör büyüdükçe en küçük alt gruptaki nokta sayısı da o derecede azalır. Nokta sayısının azalması brute force saldırısına karşı dayanıklılığı azaltır. Bu sebeple alt gruptaki nokta sayısının toplam nokta sayısına eşit olması için tek bir alt grup olması yani h=1 olması tercih edilir.
Generator Point (G)
G noktası, bitcoinde tüm public key’lerin türetildiği sabit bir başlangıç noktasıdır. Eliptik eğri hesaplamalarında her public key, aynı G noktası üzerinden türetilir. Farklı olan tek parametre private key’dir.
G noktası bir nokta olduğu için (x, y) koordinatları ile gösterilir. Bu koordinatlar; p ve n gibi oldukça büyük sayılardır. Secp256k1 eğrisinde kullanılan standart G noktasının koordinatları şöyledir;
- Gx = 79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
- Gy = 483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8
G noktasının matematiksel kaynağı
Bir noktanın bir sayı ile çarpılması, aslında o noktanın kendisiyle tekrar tekrar toplanmasıdır. Yani: P * k = P + P + P + P + …(k kez). Toplama işlemlerinin sonunda ulaştığımız Pk noktası belirli koşulların sağlanması halinde sonsuzdaki nokta (𝒪) olur. Yani;
Sonsuzdaki bu noktaya nasıl ulaşılır? Noktaları toplamaya devam ettiğimizde, Pk-1 noktası, P1’in negatifi olmuş olur ve Pk-1 noktası P1 noktasıyla son kez toplandığında Pk noktasına ulaşılır. Yani son adımda birbirinin negatifi iki nokta toplanmış olduğundan Pk noktası, sonsuzdaki nokta (𝒪) olur.
P * k = 𝒪
Uygun k değerinin seçilmesi halinde her nokta için bu denklik sağlanabilir. Yani seçilen P noktasına göre k değeri değişir.
Denkliği sağlayan (P,k) kombinasyonunda eğer “k” değeri secp256k1 eğrisi formülündeki order değerine (n) eşitse; o zaman P noktası, Generator Point (G noktası) olarak isimlendirilir. Yani;
P * k = 𝒪 ve k = n ise P = G ‘dir
Bir diğer ayrıntı da k=n olsa dahi birden fazla P noktası, denkliği sağlayabilir. Yani, k=n koşulunda bile birden fazla G noktası mevcuttur. Peki, eliptik eğri hesaplamalarında hangi G noktası kullanılmalıdır? Herhangi bir G noktası kullanılabilir. Önemli olan herkesin aynı G noktasını kullanması gerektiğidir. Çünkü public key oluşturmada ve imza doğrulamada standardizasyon için tüm hesaplamalar için aynı G noktasını kullanılmalıdır. Aksi halde farklı G noktaları kullanılırsa eliptik eğri hesaplamalarında aynı private key’den farklı public key’ler oluşur ve imza doğrulama mümkün olmaz.
G noktası nasıl seçildi?
Secp256k1 eğrisinde kullanılan ve yukarıdaki paragraflarda değerleri yazılı olan standart G noktasının koordinatları çok büyük sayılardır. 0’dan başlayıp x ve y koordinatlarını teker teker artırarak bu noktayı bulmak yıllar süreceği için imkânsızdır. Öyleyse, bu G noktası nasıl bulundu? Kısa cevap: nasıl bulunduğu bilinmemektedir.
SECG tarafından yayınlanmış SEC dökümanlarında secp256k1 eğrisi için yukarıdaki koordinatları yazılı bu G noktasının kullanılması önerilmiştir. Ancak bu G noktasının koordinatlarının nasıl bulunduğu açıklanmamıştır. SECG tarafından önerildiği için secp256k1 eğrisi için standart haline gelmiştir ve bu nedenle eğri üzerinde yapılan tüm hesaplamalar bu G noktası kullanılarak yapılmaktadır.
Standart G noktasının kaynağı net olarak bilinmediğinden arka kapı olabileceği endişesi de mevcuttur. Fakat bugüne kadar secp256k1 eğrisi ve G noktasıyla ilgili bir güvenlik açığı bulunamamıştır. Standart G noktasının kaynağından ziyade asıl önemli olan, herkesin aynı G noktasını kullanması gerektiğidir. Aksi halde standardizasyon bozulur, public key üretimi ve imza doğrulama mümkün olmaz.
Eliptik eğri parametrelerinin standardizasyonunun önemi
Yukarıdaki paragraflardaki yazılanlara göre önce (n) değeri hesaplanıp buna uygun bir G noktası seçildiği anlaşılmaktadır. Teoride böyle bir kural yoktur, ancak pratikte uygulama bu sırayladır. Yazıyı karmaşık hale getirmemek için teorik ayrıntıya değinmedik.
Eliptik eğri parametrelerinin pratikte hesaplama adımları şöyledir;
- Prime field (p) değeri için büyük bir asal sayı seçilir
- Nokta sayısı (N) hesaplanır (N; asal sayı olmalı, değilse başka p değeri denenerek tekrar N tekrar hesaplanır)
- Order değeri (n) hesaplanır (h=1 olduğundan N’ye eşit olur)
- Bir tane G noktası (G) seçilir
p, a, b, N, h, n, G; parametrelerinin hepsi sabittir. Tek farklı olan private key (d) parametresidir. Private key, genelde d harfi ile gösterilir.
p, a, b; parametrelerinden birisi değişirse prime field’daki nokta sayısı (N) değişir.
N, h; parametrelerinden birisi değişirse order değeri (n) değişir.
n; parametresi değişirse G noktası değişir.
G; değişirse private key (d)’den oluşan public key’ler değişir ve imza doğrulama yapılamaz.
İlk adımdaki p değeri başka bir asal sayı da seçilebilirdi. Hangi asal sayı seçildiğinin önemi yoktur. Önemli olan; herkesin aynı p değerini kullanması ve bu değerinin bir asal sayı olması ve brute force saldırısını önleyecek kadar büyük bir sayı olması gerektiğidir.
Seçilen p değerine göre de N ve n; parametreleri hesaplanır ve bir tane G noktası seçilir. Ardından bu parametreler standart kabul edilerek tüm eliptik eğri hesaplamaları bu standart parametrelere göre yapılır. Eğer herkes aynı p değerini kullanmaz ise standardizasyon bozulur, public key oluşturma ve imza doğrulama mümkün olmaz.
Eliptik Eğri Matematiğinin Yazılımsal Uyarlaması
Daha önce oluşturduğumuz BitcoinKeyPairGenerator.py dosyasına ek olarak EllipticCurveMath.py adlı bir dosya oluşturalım. Şimdiye kadar bahsettiğimiz sabit sayıları hatırlamak için tekrar edelim ve kod dosyasına sabitleri ekleyelim. Ayrıca noktaları oluşturmak için sınıf ekleyelim. Sonra, sayılarla ilgili fonksiyonları ekleyelim: mod alma, negatif alma ve modüler ters (inverse). Ardından, noktalar için gerekli fonksiyonları ekleyelim: negatif alma, çiftleme, toplama ve çarpma.
- 2256 -1 = FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF
- Prime field (p) = FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
- Order (n) = FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
- Gx = 79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
- Gy = 483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8
class Point:
def __init__(self, x: int, y: int):
self.x = x
self.y = y
def __eq__(self, other):
if isinstance(other, Point):
return self.x == other.x and self.y == other.y
return False
def __str__(self):
return "x: {}\ny: {}".format(hex(self.x), hex(self.y))
# prime field
p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
# order
n = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
# generator point (x,y)
G = Point(
0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798,
0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8
)
# Mod alma
def mod(a:int) -> int:
global p
return a % p
# Sayının negatifini alma
def scalar_negate(a:int) -> int:
return mod(p - mod(a))
# Moduler inverse
def inverse(a:int) -> int:
global p
m=p
original_m = m
a = a % m
if(a == 0):
return None
if(a == 1):
return 1
x1 = 0
x2 = 1
x3 = 0
q3 = m // a
r = m % a
m = a
a = r
q1 = q3
q3 = m // a
r = m % a
q2 = q3
m = a
a = r
while (r > 0):
q3 = m // a
r = m % a
x3 = (x1 - x2 * q1) % original_m
x1 = x2
x2 = x3
q1 = q2
q2 = q3
m = a
a = r
x3 = (x1 - x2 * q1) % original_m
return x3
# Noktanın negatifini alma
def point_negate(pt:Point) -> Point:
return Point(pt.x, scalar_negate(pt.y))
# Nokta çiftleme
def double(pt: Point) -> Point:
s = mod((3*pt.x**2) * inverse(2*pt.y))
x3 = mod(s**2 - 2*pt.x)
y3 = mod(pt.y + s*(x3 - pt.x))
pt3 = Point(x3,y3)
return point_negate(pt3)
# Nokta toplama
def add(pt1: Point, pt2: Point) -> Point:
if(pt1 == pt2):
return double(pt1)
s = mod((pt2.y - pt1.y) * inverse(pt2.x - pt1.x))
x3 = mod(s**2 - pt1.x - pt2.x)
y3 = mod(s*(x3 - pt1.x) + pt1.y)
pt3 = Point(x3,y3)
return point_negate(pt3)
# Skalar çarpma
def multiply(pt: Point, k:int) -> Point:
result = pt
binary = bin(k)[2:]
for b in binary[1:]:
result = double(result)
if(b == '1'):
result = add(result, pt)
return resultPublic Key Oluşturma
Public key oluşturmanın ilk adımı, G noktasının private key ile skalar çarpılmasıdır. Skalar çarpma işleminin sonucu (x, y) koordinatlarından oluşan bir noktadır. Yani;
P : public key point d : private key G : generator point
P = d * G
Public key point’ten elde edilen x ve y koordinatları hexadecimal biçimde yan yana yazılarak public key oluşturulur. Bu formata “uncompressed public key” denir. Alternatif olarak “compressed public key” de üretilebilir.
Public key’in hangi formatta olduğunu belirtmek için şu kurallar uygulanır:
– Uncompressed public key: Başına “04” yazılır, ardından “x ve y” hexadecimal değerleri başında 0x olmadan string olarak yazılır.
– Compressed public key: Sadece “x” değeri string olarak yazılır. Eğer “y” çift ise başına “02”, tek ise “03” yazılır.
Her iki durumda da sayılar hexadecimal biçimdedir. Yan yana ekleme; string birleştirmedir, matematiksel toplama değildir. X ve Y’nin string değerlerinin başında “0x” ön eki kullanılmaz.
- Public keyuncompressed : “04” + “P.x” + “P.y”
- Public keycompressed : “02” + “P.x” (P.y mod2 ≡ 0)
- Public keycompressed : “03” + “P.x” (P.y mod2 ≡ 1)
Uncompressed public key’e pratikte gerek yoktur. Çünkü x bilindiğinde eliptik eğri formülünden y değeri hesaplanabilir. Pozitif ve negatif olarak iki farklı y değeri elde edilir. Bu iki farklı y değerine önceki paragraflarda açıkladığımız şekilde modp uyguladığımızda ikisi de pozitif olur ve p’den küçük hale gelir. Biri tek biri de çift sayı olur. Hangi değerin kullanıldığı, baştaki “02” veya “03” ön ekinden anlaşılabilir.
Bu nedenle adres üretiminde genellikle compressed public key tercih edilir.
BitcoinKeyPairGenerator.py adlı kod dosyamızı aşağıdaki şekilde güncelleyelim.
import secrets
import EllipticCurveMath as ecm
def generate_private_key():
while(True):
r = secrets.randbits(256)
if(0 < r < ecm.n):
return r
def generate_public_key(private_key:int):
public_key_point = ecm.multiply(ecm.G, private_key)
x_hex = format(public_key_point.x, "064x")
y_hex = format(public_key_point.y, "064x")
uncompressed_public_key_string = f"04{x_hex}{y_hex}"
compressed_public_key_string = None
if(public_key_point.y % 2 == 0):
compressed_public_key_string = f"02{x_hex}"
else:
compressed_public_key_string = f"03{x_hex}"
return (public_key_point, uncompressed_public_key_string, compressed_public_key_string)
# private key
private_key = generate_private_key()
print("d: {}".format(hex(private_key)))
# public key
(public_key_point, uncompressed_public_key_string, compressed_public_key_string) = generate_public_key(private_key)
print(public_key_point)
print("uncompressed_public_key:\t{}".format(uncompressed_public_key_string))
print("compressed_public_key:\t{}".format(compressed_public_key_string))Address
Adresler, public key’den türetilir. Aslında bitcoin transferlerinde adres kullanmak zorunlu değildir; public key’ler de doğrudan kullanılabilir. Ancak günümüzde gizliliği artırmak, karakter sayısını kısaltmak ve okunabilirliği kolaylaştırmak için adres formatı tercih edilir.
“Adres” terimi bazen kafa karıştırıcı olabilir. Bitcoinde adres, aslında public key’den türetilmiş karakter dizisini ifade eder. Fakat bazen bitcoinin gönderileceği hedefi belirtmek için de kullanılabilir. Bu hedef genelde adres formatındadır ama public key de olabilir. Yani adres ifadesi hem public key’i hem de hem public key’den türetilmiş adresi belirtmek için kullanılabilmektedir.
Adreslerin oluşturulma yöntemlerini, adres formatlarını ve kullanım amaçlarını sonraki yazılarımızda ayrıntılarıyla ele alacağız.
(CSPRNG)
Random number
↓
Private key
↓ − Eliptik eğri
Public key
↓ − Address oluşturma yöntemleri
Address
Son Söz
Bu yazıda bitcoinin temelini oluşturan private key ve public key kavramlarını ayrıntılı şekilde ele aldık. Gelecek yazımızda adreslerden bahsedeceğiz.
Faydalı bir hayat dilerim.
